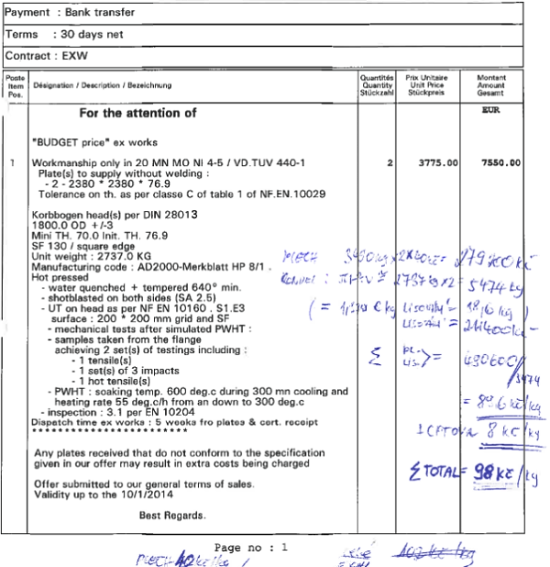
MATERIÁLY
Příklad využitelnosti plechů
Výpočet hrubé hmotnosti je základním kritériem pro rozpočtáře.
1. VÝPALKY
Tentokrát se podíváme na pár příkladů založení výpalků do formátu plechu:
* procentem odpadu je zde míněn koeficient hrubá/čistá hmotnost
FORMÁT 10x1000x2000 mm hmot. tabule ( ƍ = 7880 ) 157,6 kg
hmotnostní poměr procento odpadu*
výrobek/ výpočet
A) Obd. desky 485 x 487,5 8ks mezery 10mm
0,485 x 0,4875 x 0,01 x 7880 x 8 = 157,6 / 149,1 = 6%
B) Obd. desky 237,5 x 238,75 32ks mezery 10mm
0,2375 x 0,23875 x 0,01 x 7880 x 32 = 157,6 / 143,0 = 10%
C) Plocháče 178 x 960 10ks mezery 20mm + lem
0,178 x 0,960 x 0,01 x 7880 x 10 = 157,6 / 134,7 = 17%
D) Kruhovky Ø 225 32ks ( 4 x 8 )
3,1415 x 0,1125 2 x 0,01 x 7880 x 32 = 157,6 / 100,3 = 57%
Zde se dostáváme k pojmu IDEÁLNÍ ZALOŽENÍ PLECHU, ke kterému se blíží příklady A, B, C. Pro pálení je nutné ponechat mezery, popřípadě prostor pro nájezdy, u sil. tloušťek i pro zámky. Jsou tyto příklady pokus o přiblížení se ideálu.
V praxi však takové výpalky existují jen výjimečně, pokud pálíme i jen prosté čtverce - mřížka, která z plechu zbude tvoří 17 -20% odpadu což je jako minimum !
Zato běžným výrobkem je kruhovka, zde bylo použité nestřídavé založení, které procentuálně zcela odpovídá další běžné situaci a to nahromadění různotvarých pozic na jednom plechu nebo výpalky složitě tvarované s minimální možností založení do sebe. Odpady se zde pohybují od 50% výše !
Další příklad z praxe je odpalování hran na formátu – jen srovnávání a zaúkosování. Příklad pro náš plech:
E) Formátování tabule 10 x 1000 x 2000 1ks 10mm lem z obvodu
0,01 x 0,01 x 6 x 7880 = 4,73 kg odpad 157,6 / 134,7 = 3%
Odpady pro luby nádrží by tedy neměli činit více než 5% , ovšem pozor, záleží na užité technologii – frézování úkosů, je procento menší, ale při nestandardních formátech - třeba doměrky - šíře poslední vrstvy 1250 mm, nebo vypalování otvoru pro průlezy a nátrubky už toto procento mění.
Obecně známá jsou schémata jednotlivých případů - jako pálení mezikruží, kruhovky ze čtverce aj.
F) Kruhovka ze čtverce dle teorie (bez lemu) = 28%
Kruhovka ze čtverce dle praxe ( s lemem) = 30%
Další kapitolou obecně známých schémat jsou konusy nebo zkružovaná kolena ze segmentů. Konstrukčně klesá míra odpadu s nárůstem strmosti kužele a obráceně, záleží na počtu segmentů a využitelnosti formátu plechu.
G) Konus 10 – 45 ST do šíře formátu 3,5 m = 30% - 60%
Konus 45 – 80 ST do šíře formátu 3,5 m = 60% - 90%
Specifickým příkladem je i pálení mezikruží velkých přírub - pokud je ze segmentů opět hraje roli založení /formát /tloušťka 50% - 100%
U mezikruží pálených vcelku je odpadem celý čtverec plus kruh co vypadne ze středu, teď je otázka je-li další využití pro tento materiál anebo ne, zda ho zákazníkovi účtovat nebo neúčtovat. V praxi to dopadne stejně tak, že buď je z toho šrot, nebo v lepším případě se nám ve skladě válí cela řada zbytků, pro které využití stejně nebude nalezeno. Měli bychom do nákladů na materiál počítat plnou hmotnost plechu, který bude nakoupen, jinak při párovaní faktur vznikne na zakázce nepokrytý stav = manko. Aby byl takový výpočet fér nezapomeneme od ceny materiálu odečíst cenu za hmotnost šrotu. Víc se v tomto případě nedá udělat.
Třeba posuzovat případ od případu jako v tomto příkladě:
Zákazník potřeboval obdélníky z plechu 2x1m o délce 1333 mm
H) Obdélník 10 x 1000 x 1333 což jsou 2/3 naší tabule = 157,6 / 105kg = 50%
Zbývající obdélník je ještě pěkně využitelný kus plechu, takže počítat celou tabuli nebo nepočítat? Při 200ks už to budete muset řešit, pokud toto nelze pokrýt jiným výhodným formátem – svitek nebo rozměr z výroby (za vyšší cenu ovšem ) jako jedna z variant se nabízí řešení s tím, že zákazník si zbytky odveze... a vy fakturujete tolik tabulí, kolik bylo koupeno bez vratek na sklad. To je ale jen teorie, tento rozdíl může totiž být rozhodujícím kritériem pro výhru VŘ a pak se třeba bude počítat jen čistá spotřeba plechu a zbytky půjdou do skladu... Je to tedy na zvážení celkové situace.
Závěr. Rozpočtář by se neměl spoléhat jen na obecně platná schémata pro hrubé hmotnosti materiálu, ale vždy se snažit tuto hmotnost přepočítat s ohledem na použitý výchozí rozměr skutečně nakoupeného polotovaru !
Pozn. 1: Uvedená procenta odpovídají tomu, jaký základ byl zvolen při výpočtu. Zvolením za základ – buď plech, nebo propal, výrobek dostaneme hodnoty, které se budou lišit.
POZOR! Zde je všude „procentem odpadu“ míněná hodnota, o kterou musíme navýšit čistou hmotnost výrobku, abychom dostali hrubou hmotnost výchozího polotovaru kterým je daný plech. Není to tedy procento odpadu z plechu jako takového, viz třeba znovu příklad D,:
D) Kruhovky Ø 225 32ks ( 4 x 8 )
3,1415 x 0,1125 2 x 0,01 x 7880 x 32 = 157,6 / 100,3 = 57%
Čili mám-li na výkrese č. hm. těchto výrobků 100,3 kg pak je nutno vynásobit tuto hmotnost x cca 1,57 za předpokladu, že se položky do té tabule vejdou a to je třeba si spočítat. Podělením hmotností tabulí (hrubá) hmotností výrobků (čistá) dostaneme tento opravný koeficient, nelze tyto koeficienty dávat bez rozmyslu a bez potřebného ověření, což je účelem celé této ukázky.
Skutečné procento odpadu z tohoto plechu je pak (157,3-100,3= váha šrotu)/1,573 = 36,2% , procento na výrobek je 63,8 což obojí dává do hromady rovných 100%.
Vyzkoušejte si to až do konce: Cena tabule S235 je 14 Kč/kg tedy 2202 Kč
z toho výpalky 1404 Kč a šrot 798 Kč. Za šrot (57kg) dostaneme 6 Kč/kg je tedy správná cena za materiál 2202 – 342 Kč = 1860 Kč. Potom následuje výroba, režije, spotřebka, marže a popřípadě doprava. Pálení např. = 16Kč/kg tedy celkem výpalky = 3465 Kč x cca 1,247 (všecko ostatní) = 4320 Kč prodejní cena. 1ks tedy výjde na 135 Kč, což je 43,07 Kč/kg za tyto výpalky.
Pozn. 2: Měrná hmotnost plechu je zde užitá 7880 kg/m3 kterou používám jako rozpočtářskou, ve skutečnosti je to pak pro ocel s 0,2% C 7850 kg/m3. Někteří prvovýrobci plechů se s tím nemažou a počítají na faktury 8000 kg/m3 u běžných jakostí! Což odpovídá spíše měrným hmotnostem nerez ocelí !!! Při inventurách a reálném tárování skladu tak vzniká nesoulad, který se za pár let projeví pořádným mankem!!! Řešení tohoto problému nebylo nalezeno…
2. VÝLISKY - KLENUTÁ DNA
Výpočet hrubé hmotnosti výlisků den:
Na internetu koluje mnoho různých rovnic pro výpočet čisté hmotnosti dna (z jeho rozměrů !), např:
M =m1 (rondel) + m2 (košilka, trubka, lem dna)
M= π(r*1,234)2 *v * 7880 * + (π*D*v*t*7880) což nedává dobrý výsledek, protože poměr průměru rondelu vůči radiusu jeho hrany neroste lineárně. Používáme proto výhradně Guldinovy věty a výpočet se vztahuje na střední vlákno.
Je-li ale známa čistá hmotnost výlisku dna, pak je možné snadno zjistit minimální rozměr kruhovky, ze které byl pořízen.
Vzorec pro výpočet průměru výchozí kruhovky dna známe–li hmotnost.
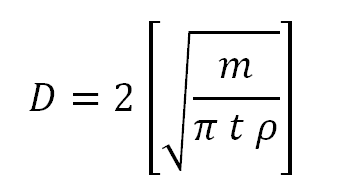
m je hmotnost výlisku, t je tloušťka materiálu a p je měrná hmotnost oceli
V praxi to ovšem zase není konečný rozměr kruhovky, ale opsaného čtverce, kterýžto výrobce logicky počítá jako spotřebu materiálu na výrobu výlisku. Výchozím polotovarem je tedy v případě obyčejného klenutého dna čtverec, v případě dna s vyššími požadavky na jakost obdélník s připojenými zkušebními deskami, které projdou stejným tepelným zpracováním jako vlastní dno. Navýšení hrubé hm. vůči čisté tedy činí 30 až 40%.
Dno se zkušebními deskami:
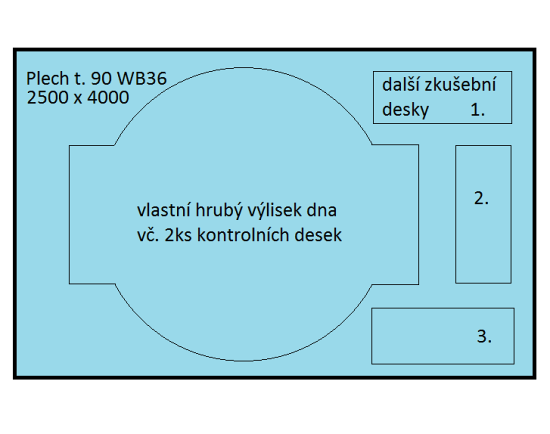
Hrubé hmotnosti, částečně očištěné od obdélníkových odpadů jsou i v příslušných DIN normách. 3D Modelováním v Solidu bylo zjištěno, že uváděné hodnoty neodpovídají hmotnostem přesnému 3D modelu, pravděpodobně tedy obsahují přídavek na okolek kruhovky. Jak bylo těchto tabulek dosaženo není známo, přesto jsou pro použití vhodné.
Náhled norem DIN28011 pro torisférická dna a DIN28013 pro eliptická:


Vlastní výpočet kilogramové ceny dle přijaté nabídky se liší především o cenu dopravy, která se rozkládá na počet kusů. Proto cena u stejných den nebude stejná, záleží na dalších okolnostech objednávky, kusy, bonitní ujednání a jiné vlivy. Tak to potom vypadá kontrola v praxi na přijaté nabídce: